CHAPTER 6
BLACK HOLES
The term black hole is of very recent origin. It was coined in 1969 by the American scientist John Wheeler as a graphic description of an idea that goes back at least two hundred years, to a time when there were two theories about light: one, which Newton favored, was that it was composed of particles; the other was that it was made of waves. We now know that really both theories are correct. By the wave/particle duality of quantum mechanics, light can be regarded as both a wave and a particle. Under the theory that light is made up of waves, it was not clear how it would respond to gravity. But if light is composed of particles, one might expect them to be affected by gravity in the same way that cannonballs, rockets, and planets are. At first people thought that particles of light traveled infinitely fast, so gravity would not have been able to slow them down, but the discovery by Roemer that light travels at a finite speed meant that gravity might have an important effect.
On this assumption, a Cambridge don, John Michell, wrote a paper in 1783 in the Philosophical Transactions of the Royal Society of London in which he pointed out that a star that was sufficiently massive and compact would have such a strong gravitational field that light could not escape: any light emitted from the surface of the star would be dragged back by the star’s gravitational attraction before it could get very far. Michell suggested that there might be a large number of stars like this. Although we would not be able to see them because the light from them would not reach us, we would still feel their gravitational attraction. Such objects are what we now call black holes, because that is what they are: black voids in space. A similar suggestion was made a few years later by the French scientist the Marquis de Laplace, apparently independently of Michell. Interestingly enough, Laplace included it in only the first and second editions of his book The System of the World, and left it out of later editions; perhaps he decided that it was a crazy idea. (Also, the particle theory of light went out of favor during the nineteenth century; it seemed that everything could be explained by the wave theory, and according to the wave theory, it was not clear that light would be affected by gravity at all.)
In fact, it is not really consistent to treat light like cannonballs in Newton’s theory of gravity because the speed of light is fixed. (A cannonball fired upward from the earth will be slowed down by gravity and will eventually stop and fall back; a photon, however, must continue upward at a constant speed. How then can Newtonian grav-ity affect light?) A consistent theory of how gravity affects light did not come along until Einstein proposed general relativity in 1915. And even then it was a long time before the implications of the theory for massive stars were understood.
To understand how a black hole might be formed, we first need an understanding of the life cycle of a star. A star is formed when a large amount of gas (mostly hydrogen) starts to collapse in on itself due to its gravitational attraction. As it contracts, the atoms of the gas collide with each other more and more frequently and at greater and greater speeds – the gas heats up. Eventually, the gas will be so hot that when the hydrogen atoms collide they no longer bounce off each other, but instead coalesce to form helium. The heat released in this reaction, which is like a controlled hydrogen bomb explosion, is what makes the star shine. This additional heat also increases the pressure of the gas until it is sufficient to balance the gravitational attraction, and the gas stops contracting. It is a bit like a balloon – there is a balance between the pressure of the air inside, which is trying to make the balloon expand, and the tension in the rubber, which is trying to make the balloon smaller. Stars will remain stable like this for a long time, with heat from the nuclear reactions balancing the gravitational attraction. Eventually, however, the star will run out of its hydrogen and other nuclear fuels. Paradoxically, the more fuel a star starts off with, the sooner it runs out. This is because the more massive the star is, the hotter it needs to be to balance its gravitational attraction. And the hotter it is, the faster it will use up its fuel. Our sun has probably got enough fuel for another five thousand million years or so, but more massive stars can use up their fuel in as little as one hundred million years, much less than the age of the universe. When a star runs out of fuel, it starts to cool off and so to contract. What might happen to it then was first understood only at the end of the 1920s.
In 1928 an Indian graduate student, Subrahmanyan Chandrasekhar, set sail for England to study at Cambridge with the British astronomer Sir Arthur Eddington, an expert on general relativity. (According to some accounts, a journalist told Eddington in the early 1920s that he had heard there were only three people in the world who understood general relativity. Eddington paused, then replied, “I am trying to think who the third person is.”) During his voyage from India, Chandrasekhar worked out how big a star could be and still support itself against its own gravity after it had used up all its fuel. The idea was this: when the star becomes small, the matter particles get very near each other, and so according to the Pauli exclusion principle, they must have very different velocities. This makes them move away from each other and so tends to make the star expand. A star can therefore maintain itself at a constant radius by a balance between the attraction of gravity and the repulsion that arises from the exclusion principle, just as earlier in its life gravity was balanced by the heat.
Chandrasekhar realized, however, that there is a limit to the repulsion that the exclusion principle can provide. The theory of relativity limits the maximum difference in the velocities of the matter particles in the star to the speed of light. This means that when the star got sufficiently dense, the repulsion caused by the exclusion principle would be less than the attraction of gravity. Chandrasekhar calculated that a cold star of more than about one and a half times the mass of the sun would not be able to support itself against its own gravity. (This mass is now known as the Chandrasekhar limit.) A similar discovery was made about the same time by the Russian scientist Lev Davidovich Landau.
This had serious implications for the ultimate fate of massive stars. If a star’s mass is less than the Chandrasekhar limit, it can eventually stop contracting and settle down to a possible final state as a “white dwarf” with a radius of a few thousand miles and a density of hundreds of tons per cubic inch. A white dwarf is supported by the exclusion principle repulsion between the electrons in its matter. We observe a large number of these white dwarf stars. One of the first to be discovered is a star that is orbiting around Sirius, the brightest star in the night sky.
Landau pointed out that there was another possible final state for a star, also with a limiting mass of about one or two times the mass of the sun but much smaller even than a white dwarf. These stars would be supported by the exclusion principle repulsion between neutrons and protons, rather than between electrons. They were therefore called neutron stars. They would have a radius of only ten miles or so and a density of hundreds of millions of tons per cubic inch. At the time they were first predicted, there was no way that neutron stars could be observed. They were not actually detected until much later.
Stars with masses above the Chandrasekhar limit, on the other hand, have a big problem when they come to the end of their fuel. In some cases they may explode or manage to throw off enough matter to reduce their mass below the limit and so avoid catastrophic gravitational collapse, but it was difficult to believe that this always happened, no matter how big the star. How would it know that it had to lose weight? And even if every star managed to lose enough mass to avoid collapse, what would happen if you added more mass to a white dwarf 'or neutron star to take it over the limit? Would it collapse to infinite density? Eddington was shocked by that implication, and he refused to believe Chandrasekhar’s result. Eddington thought it was simply not possible that a star could collapse to a point. This was the view of most scientists: Einstein himself wrote a paper in which he claimed that stars would not shrink to zero size. The hostility of other scientists, particularly Eddington, his former teacher and the leading authority on the structure of stars, persuaded Chandrasekhar to abandon this line of work and turn instead to other problems in astronomy, such as the motion of star clusters. However, when he was awarded the Nobel Prize in 1983, it was, at least in part, for his early work on the limiting mass of cold stars.
Chandrasekhar had shown that the exclusion principle could not halt the collapse of a star more massive than the Chandrasekhar limit, but the problem of understanding what would happen to such a star, according to general relativity, was first solved by a young American, Robert Oppenheimer, in 1939. His result, however, suggested that there would be no observational consequences that could be detected by the telescopes of the day. Then World War II intervened and Oppenheimer himself became closely involved in the atom bomb project. After the war the problem of gravitational collapse was largely forgotten as most scientists became caught up in what happens on the scale of the atom and its nucleus. In the 1960s, however, interest in the large-scale problems of astronomy and cosmology was revived by a great increase in the number and range of astronomical observations brought about by the application of modern technology. Oppenheimer’s work was then rediscovered and extended by a number of people.
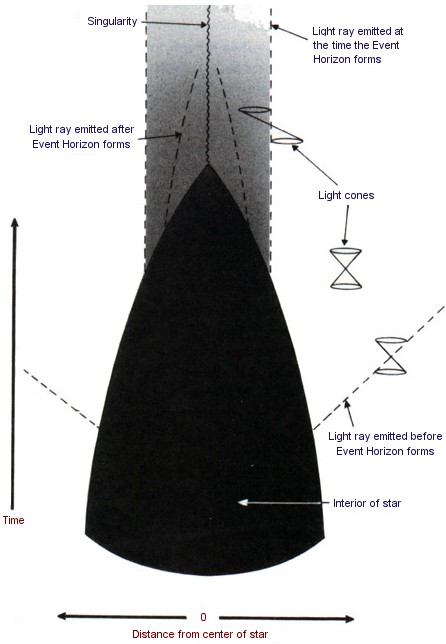
The picture that we now have from Oppenheimer’s work is as follows. The gravitational field of the star changes the paths of light rays in space-time from what they would have been had the star not been present. The light cones, which indicate the paths followed in space and time by flashes of light emitted from their tips, are bent slightly inward near the surface of the star. This can be seen in the bending of light from distant stars observed during an eclipse of the sun. As the star contracts, the gravitational field at its surface gets stronger and the light cones get bent inward more. This makes it more difficult for light from the star to escape, and the light appears dimmer and redder to an observer at a distance. Eventually, when the star has shrunk to a certain critical radius, the gravitational field at the surface becomes so strong that the light cones are bent inward so much that light can no longer escape Figure 6:1.
 |
Figure 6:1
According to the theory of relativity, nothing can travel faster than light. Thus if light cannot escape, neither can anything else; everything is dragged back by the gravitational field. So one has a set of events, a region of space-time, from which it is not possible to escape to reach a distant observer. This region is what we now call a black hole. Its boundary is called the event horizon and it coincides with the paths of light rays that just fail to escape from the black hole.
In order to understand what you would see if you were watching a star collapse to form a black hole, one has to remember that in the theory of relativity there is no absolute time. Each observer has his own measure of time. The time for someone on a star will be different from that for someone at a distance, because of the gravitational field of the star. Suppose an intrepid astronaut on the surface of the collapsing star, collapsing inward with it, sent a signal every second, according to his watch, to his spaceship orbiting about the star. At some time on his watch, say 11:00, the star would shrink below the critical radius at which the gravitational field becomes so strong nothing can escape, and his signals would no longer reach the spaceship. As 11:00 approached his companions watching from the spaceship would find the intervals between successive signals from the astronaut getting longer and longer, but this effect would be very small before 10:59:59. They would have to wait only very slightly more than a second between the astronaut’s 10:59:58 signal and the one that he sent when his watch read 10:59:59, but they would have to wait forever for the 11:00 signal. The light waves emitted from the surface of the star between 10:59:59 and 11:00, by the astronaut’s watch, would be spread out over an infinite period of time, as seen from the spaceship. The time interval between the arrival of successive waves at the spaceship would get longer and longer, so the light from the star would appear redder and redder and fainter and fainter. Eventually, the star would be so dim that it could no longer be seen from the spaceship: all that would be left would be a black hole in space. The star would, however, continue to exert the same gravitational force on the spaceship, which would continue to orbit the black hole. This scenario is not entirely realistic, however, because of the following problem. Gravity gets weaker the farther you are from the star, so the gravitational force on our intrepid astronaut’s feet would always be greater than the force on his head. This difference in the forces would stretch our astronaut out like spaghetti or tear him apart before the star had contracted to the critical radius at which the event horizon formed! However, we believe that there are much larger objects in the universe, like the central regions of galaxies, that can also undergo gravitational collapse to produce black holes; an astronaut on one of these would not be torn apart before the black hole formed. He would not, in fact, feel anything special as he reached the critical radius, and could pass the point of no return without noticing it However, within just a few hours, as the region continued to collapse, the difference in the gravitational forces on his head and his feet would become so strong that again it would tear him apart.
The work that Roger Penrose and I did between 1965 and 1970 showed that, according to general relativity, there must be a singularity of infinite density and space-time curvature within a black hole. This is rather like the big bang at the beginning of time, only it would be an end of time for the collapsing body and the astronaut. At this singularity the laws of science and our ability to predict the future would break down. However, any observer who remained outside the black hole would not be affected by this failure of predictability, because neither light nor any other signal could reach him from the singularity. This remarkable fact led Roger Penrose to propose the cosmic censorship hypothesis, which might be paraphrased as “God abhors a naked singularity.” In other words, the singularities produced by gravitational collapse occur only in places, like black holes, where they are decently hidden from outside view by an event horizon. Strictly, this is what is known as the weak cosmic censorship hypothesis: it protects observers who remain outside the black hole from the consequences of the breakdown of predictability that occurs at the singularity, but it does nothing at all for the poor unfortunate astronaut who falls into the hole.
There are some solutions of the equations of general relativity in which it is possible for our astronaut to see a naked singularity: he may be able to avoid hitting the singularity and instead fall through a "wormhole” and come out in another region of the universe. This would offer great possibilities for travel in space and time, but unfortunately it seems that these solutions may all be highly unstable; the least disturbance, such as the presence of an astronaut, may change them so that the astronaut could not see the singularity until he hit it and his time came to an end. In other words, the singularity would always lie in his future and never in his past. The strong version of the cosmic censorship hypothesis states that in a realistic solution, the singularities would always lie either entirely in the future (like the singularities of gravitational collapse) or entirely in the past (like the , big bang). I strongly believe in cosmic censorship so I bet Kip Thorne and John Preskill of Cal Tech that it would always hold. I lost the bet on a technicality because examples were produced of solutions with a singularity that was visible from a long way away. So I had to pay up, which according to the terms of the bet meant I had to clothe their nakedness. But I can claim a moral victory. The naked singularities were unstable: the least disturbance would cause them either to disappear or to be hidden behind an event horizon. So they would not occur in realistic situations.
The event horizon, the boundary of the region of space-time from which it is not possible to escape, acts rather like a one-way membrane around the black hole: objects, such as unwary astronauts, can fall through the event horizon into the black hole, but nothing can ever get out of the black hole through the event horizon. (Remember that the event horizon is the path in space-time of light that is trying to escape from the black hole, and nothing can travel faster than light.) One could well say of the event horizon what the poet Dante said of the entrance to Hell: “All hope abandon, ye who enter here.” Anything or anyone who falls through the event horizon will soon reach the region of infinite density and the end of time.
General relativity predicts that heavy objects that are moving will cause the emission of gravitational waves, ripples in the curvature of space that travel at the speed of light. These are similar to light waves, which are ripples of the electromagnetic field, but they are much harder to detect. They can be observed by the very slight change in separation they produce between neighboring freely moving objects. A number of detectors are being built in the United States, Europe, and Japan that will measure displacements of one part in a thousand million million million (1 with twenty-one zeros after it), or less than the nucleus of an atom over a distance of ten miles.
Like light, gravitational waves carry energy away from the objects that emit them. One would therefore expect a system of massive objects to settle down eventually to a stationary state, because the energy in any movement would be carried away by the emission of gravitational waves. (It is rather like dropping a cork into water: at first it bobs up and down a great deal, but as the ripples carry away its energy, it eventually settles down to a stationary state.) For example, the movement of the earth in its orbit round the sun produces gravitational waves. The effect of the energy loss will be to change the orbit of the earth so that gradually it gets nearer and nearer to the sun, eventually collides with it, and settles down to a stationary state. The rate of energy loss in the case of the earth and the sun is very low – about enough to run a small electric heater. This means it will take about a thousand million million million million years for the earth to run into the sun, so there’s no immediate cause for worry! The change in the orbit of the earth is too slow to be observed, but this same effect has been observed over the past few years occurring in the system called PSR 1913 + 16 (PSR stands for “pulsar,” a special type of neutron star that emits regular pulses of radio waves). This system contains two neutron stars orbiting each other, and the energy they are losing by the emission of gravitational waves is causing them to spiral in toward each other. This confirmation of general relativity won J. H. Taylor and R. A. Hulse the Nobel Prize in 1993. It will take about three hundred million . years for them to collide. Just before they do, they will be orbiting so fast that they will emit enough gravitational waves for detectors like LIGO to pick up.
During the gravitational collapse of a star to form a black hole, the movements would be much more rapid, so the rate at which energy is carried away would be much higher. It would therefore not be too long ' before it settled down to a stationary state. What would this final stage look like? One might suppose that it would depend on all the complex features of the star from which it had formed – not only its mass and rate of rotation, but also the different densities of various parts of the star, and the complicated movements of the gases within the star. And if black holes were as varied as the objects that collapsed to form them, it might be very difficult to make any predictions about black holes in general.
In 1967, however, the study of black holes was revolutionized by Werner Israel, a Canadian scientist (who was born in Berlin, brought up in South Africa, and took his doctoral degree in Ireland). Israel showed that, according to general relativity, non-rotating black holes must be very simple; they were perfectly spherical, their size depended only on their mass, and any two such black holes with the same mass were identical. They could, in fact, be described by a particular solution of Einstein’s equations that had been known since 1917, found by Karl Schwarzschild shortly after the discovery of general relativity. At first many people, including Israel himself, argued that since black holes had to be perfectly spherical, a black hole could only form from the collapse of a perfectly spherical object. Any real star – which would never be perfectly spherical – could therefore only collapse to form a naked singularity.
There was, however, a different interpretation of Israel’s result, which was advocated by Roger Penrose and John Wheeler in particular. They argued that the rapid movements involved in a star’s collapse would mean that the gravitational waves it gave off would make it ever more spherical, and by the time it had settled down to a stationary state, it would be precisely spherical. According to this view, any non-rotating star, however complicated its shape and internal structure, would end up after gravitational collapse as a perfectly spherical black hole, whose size would depend only on its mass. Further calculations supported this view, and it soon came to be adopted generally.
Israel’s result dealt with the case of black holes formed from non-rotating bodies only. In 1963, Roy Kerr, a New Zealander, found a set of solutions of the equations of general relativity that described rotating black holes. These “Kerr” black holes rotate at a constant rate, their size and shape depending only on their mass and rate of rotation. If the rotation is zero, the black hole is perfectly round and the solution is identical to the Schwarzschild solution. If the rotation is non-zero, the black hole bulges outward near its equator (just as the earth or the sun bulge due to their rotation), and the faster it rotates, the more it bulges. So, to extend Israel’s result to include rotating bodies, it was conjectured that any rotating body that collapsed to form a black hole would eventually settle down to a stationary state described by the Kerr solution. In 1970 a colleague and fellow research student of mine at Cambridge, Brandon Carter, took the first step toward proving this conjecture. He showed that, provided a stationary rotating black hole had an axis of symmetry, like a spinning top, its size and shape would depend only on its mass and rate of rotation. Then, in 1971, I proved that any stationary rotating black hole would indeed have such an axis of symmetry. Finally, in 1973, David Robinson at Kings College, London, used Carter’s and my results to show that the conjecture had been correct: such a black hole had indeed to be the Kerr solution. So after gravitational collapse a black hole must settle down into a state in which it could be rotating, but not pulsating. Moreover, its size and shape would depend only on its mass and rate of rotation, and not on the nature of the body that had collapsed to form it. This result became known by the maxim: “A black hole has no hair.” The “no hair” theorem is of great practical importance, because it so greatly restricts the possible types of black holes. One can therefore make detailed models of objects that might contain black holes and compare the predictions of the models with observations. It also means that a very large amount of information about the body that has collapsed must be lost when a black hole is formed, because afterward all we can possibly measure about the body is its mass and rate of rotation. The significance of this will be seen in the next chapter.
Black holes are one of only a fairly small number of cases in the history of science in which a theory was developed in great detail as a mathematical model before there was any evidence from observations that it was correct. Indeed, this used to be the main argument of opponents of black holes: how could one believe in objects for which the only evidence was calculations based on the dubious theory of general relativity? In 1963, however, Maarten Schmidt, an astronomer at the Palomar Observatory in California, measured the red shift of a faint starlike object in the direction of the source of radio waves called 3C273 (that is, source number 273 in the third Cambridge catalogue of radio sources). He found it was too large to be caused by a gravitational field: if it had been a gravitational red shift, the object would have to be so massive and so near to us that it would disturb the orbits of planets in the Solar System. This suggested that the red shift was instead caused by the expansion of the universe, which, in turn, meant that the object was a very long distance away. And to be visible at such a great distance, the object must be very bright, must, in other words, be emitting a huge amount of energy. The only mechanism that people could think of that would produce such large quantities of energy seemed to be the gravitational collapse not just of a star but of a whole central region of a galaxy. A number of other similar “quasi-stellar objects,” or quasars, have been discovered, all with large red shifts. But they are all too far away and therefore too difficult to observe to provide conclusive evidence of black holes.
Further encouragement for the existence of black holes came in 1967 with the discovery by a research student at Cambridge, Jocelyn Bell-Burnell, of objects in the sky that were emitting regular pulses of radio waves. At first Bell and her supervisor, Antony Hewish, thought they might have made contact with an alien civilization in the galaxy! Indeed, at the seminar at which they announced their discovery, I remember that they called the first four sources to be found LGM 1 – 4, LGM standing for “Little Green Men.” In the end, however, they and everyone else came to the less romantic conclusion that these objects, which were given the name pulsars, were in fact rotating neutron stars that were emitting pulses of radio waves because of a complicated interaction between their magnetic fields and surrounding matter. This was bad news for writers of space westerns, but very hopeful for the small number of us who believed in black holes at that time: it was the first positive evidence that neutron stars existed. A neutron star has a radius of about ten miles, only a few times the critical radius at which a star becomes a black hole. If a star could collapse to such a small size, it is not unreasonable to expect that other stars could collapse to even smaller size and become black holes.
How could we hope to detect a black hole, as by its very definition it does not emit any light? It might seem a bit like looking for a black cat in a coal cellar. Fortunately, there is a way. As John Michell pointed out in his pioneering paper in 1783, a black hole still exerts a gravitational fierce on nearby objects. Astronomers have observed many systems in which two stars orbit around each other, attracted toward each other by gravity. They also observe systems in which there is only one visible star that is orbiting around some unseen companion. One cannot, of course, immediately conclude that the companion is a black hole: it might merely be a star that is too faint to be seen. However, some of these systems, like the one called Cygnus X-1 Figure 6:2, are also strong sources of X-rays.
 |
Figure 6:2
The best explanation for this phenomenon is that matter has been blown off the surface of the visible star. As it falls toward the unseen companion, it develops a spiral motion (rather like water running out of a bath), and it gets very hot, emitting X-rays Figure 6:3.
 |
Figure 6:3
For this mechanism to work, the unseen object has to be very small, like a white dwarf, neutron star, or black hole. From the observed orbit of the visible star, one can determine the lowest possible mass of the unseen object. In the case of Cygnus X-l, this is about six times the mass of the sun, which, according to Chandrasekhar’r result, is too great for the unseen object to be a white dwarf. It is also too large a mass to be a neutron star. It seems, therefore, that it must be a black hole.
There are other models to explain Cygnus X-1 that do not include a black hole, but they are all rather far-fetched. A black hole seems to be the only really natural explanation of the observations. Despite this, I had a bet with Kip Thorne of the California Institute of Technology that in fact Cygnus X-1 does not contain a black hole! This was a form f insurance policy for me. I have done a lot of work on black holes, and it would all be wasted if it turned out that black holes do not exist. But in that case, I would have the consolation of winning my bet, which would bring me four years of the magazine Private Eye. In fact, although the situation with Cygnus X-1 has not changed much since we made the bet in 1975, there is now so much other observational evidence in favor of black holes that I have conceded the bet. I paid the specified penalty, which was a one-year subscription to Penthouse, to the outrage of Kip’s liberated wife.
We also now have evidence for several other black holes in systems like Cygnus X-1 in our galaxy and in two neighboring galaxies called the Magellanic Clouds. The number of black holes, however, is almost certainly very much higher; in the long history of the universe, many stars must have burned all their nuclear fuel and have had to collapse. The number of black holes may well be greater even than the number of visible stars, which totals about a hundred thousand million in our galaxy alone. The extra gravitational attraction of such a large number of black holes could explain why our galaxy rotates at the rate it does: the mass of the visible stars is insufficient to account for this. We also have some evidence that there is a much larger black hole, with a mass of about a hundred thousand times that of the sun, at the center of our galaxy. Stars in the galaxy that come too near this black hole will be torn apart by the difference in the gravitational forces on their near and far sides. Their remains and gas that is thrown off other stars, will fall toward the black hole. As in the case of Cygnus X-l, the gas will spiral inward and will heat up, though not as much as in that case. It will not get hot enough to emit X rays, but it could account for the very compact source of radio waves and infrared rays that is observed at the galactic center.
It is thought that similar but even larger black holes, with masses of about a hundred million times the mass of the sun, occur at the centers of quasars. For example, observations with the Hubble telescope of the galaxy known as M87 reveal that it contains a disk of gas 130 light-years across rotating about a central object two thousand million times the mass of the sun. This can only be a black hole. Matter falling into such a supermassive black hole would provide the only source of power great enough to explain the enormous amounts of energy that these objects are emitting. As the matter spirals into the black hole, it would make the black hole rotate in the same direction, causing it to develop a magnetic field rather like that of the earth. Very high-energy particles would be generated near the black hole by the in-falling matter. The magnetic field would be so strong that it could focus these particles into jets ejected outward along the axis of rotation of the black hole, that is, in the directions of its north and south poles. Such jets are indeed observed in a number of galaxies and quasars. One can also consider the possibility that there might be black holes with masses much less than that of the sun. Such black holes could not be formed by gravitational collapse, because their masses are below the Chandrasekhar mass limit: stars of this low mass can support themselves against the force of gravity even when they have exhausted their nuclear fuel. Low-mass black holes could form only if matter was compressed to enormous densities by very large external pressures. Such conditions could occur in a very big hydrogen bomb: the physicist John Wheeler once calculated that if one took all the heavy water in all the oceans of the world, one could build a hydrogen bomb that would compress matter at the center so much that a black hole would be created. (Of course, there would be no one left to observe it!) A more practical possibility is that such low-mass black holes might have been formed in the high temperatures and pressures of the very early universe. Black holes would have been formed only if the early universe had not been perfectly smooth and uniform, because only a small region that was denser than average could be compressed in this way to form a black hole. But we know that there must have been some irregularities, because otherwise the matter in the universe would still be perfectly uniformly distributed at the present epoch, instead of being clumped together in stars and galaxies.
Whether the irregularities required to account for stars and galaxies would have led to the formation of a significant number of “primordial” black holes clearly depends on the details of the conditions in the early universe. So if we could determine how many primordial black holes there are now, we would learn a lot about the very early stages of the universe. Primordial black holes with masses more than a thousand million tons (the mass of a large mountain) could be detected only by their gravitational influence on other, visible matter or on the expansion of the universe. However, as we shall learn in the next chapter, black holes are not really black after all: they glow like a hot body, and the smaller they are, the more they glow. So, paradoxically, smaller black holes might actually turn out to be easier to detect than large ones!